[물리] 속도와 가속도 - 가속도와 등가속도 직선 운동

가속도는 물체의 속도가 시간에 따라 변화된 정도를 나타낸 값입니다.
어떤 물체가 1초동안 얼마나 이동했는지 보고 싶으면 가속도를 보면 됩니다.

즉, 기준을 1초로 잡고 1초에 2m씩 간다고 하면
1초는 2m
2초는 4m
3초는 6m....
이런식으로 가속도가 일정한 것이 등가속도 직선 운동입니다.

가속도는 다음과 같이 구할 수 있습니다.

\( a = \frac{v-v_{0}{t} \) (단위 : \( m/s^{2} \) )

 

[그림 1] 등가속도 운동의 가속도 - 시간 그래프

등가속도 운동의 가속도 - 시간 그래프입니다.

가속도가 일정하기 때문에 이런 그래프가 그려집니다. 여기서 면적은 속도 증가량입니다.

[그림 2] 등가속도 운동의 속도 - 시간 그래프

등가속도 운동의 속도 - 시간 그래프입니다.

속도 - 시간 그래프에서의 면적은 변위입니다.

[그림 3] 등가속도 운동의 위치 - 시간 그래프

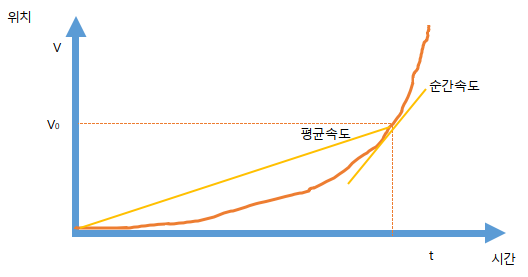
등가속도 운동의 위치 - 시간 그래프입니다.

가속도가 일정해서 속도가 계속 증가하기 때문에 이런 그래프가 그려집니다.

어느 한 점에서의 접선의 기울기는 순간 속도이고,

어느 한 점과 원점을 이은 직선의 기울기는 평균 속도입니다.

 

여기서 세 가지 공식이 나옵니다.

$$ v = v_{0} + at $$

$$ s = v_{0}t + \frac{1}{2}at^{2} $$

$$ 2as = v^{2} - v_{0}^{2} $$

등가속도 직선 운동에서 중요하게 사용되는 식입니다.

 

첫 번째 공식은 가속도 식에서부터 나옵니다.

\( a = \frac{v-v_{0}}{t} \)

양변에 t를 곱합니다.

\( at = v-v_{0} \)

v만 놔두고 모두 이항하면

\( v = v_{0} + at \)

이렇게 됩니다.

 

두 번째 공식은 등가속도 운동의 속도 - 시간 그래프에서 나옵니다.

[그림 4] 등가속도 운동위 속도 - 시간 그래프에서 변위를 구하는 모습

속도 - 시간 그래프에서의 면적은 변위입니다.

\( V_{0}t \)는 그대로니 삼각형 부분만 보면 됩니다.

\( \frac{1}{2} \times t \times (v - v_{0}) \)

여기에 \( \frac{1}{t^{2}} \) 를 곱합니다. 없는 것을 곱했으니 뒤에는 \( t^{2} \)를 곱해야 합니다.

\( \frac{1}{2} \times \frac{t(v - v_{0})}{t^{2}} \times t^{2} \)

약분시키면

\( \frac{1}{2} \times \frac{v - v_{0}}{t} \times t^{2} \)

이렇게 됩니다.

여기서 두번째 항은 가속도 구하는 식과 동일하므로

\( \frac{1}{2} \times a \times t^{2} \)

앞의 \( V_{0}t \)까지 더해주면

\( V_{0}t + \frac{1}{2} \times a \times t^{2} \)

최종 식이 나옵니다.

 

세 번째 식은 첫 번째 식과 두 번째 식을 연립해 t(시간)값을 제거한 식입니다.

연립하면 \( 2as = v^{2} - v_{0}^{2} \) 이렇게 나옵니다.