[Algorithm] Dynamic Programming(동적 계획법)과 피보나치 수열

Dynamic Programming(DP, 동적 계획법)은 큰 문제를 작은 문제들로 분할하여 문제를 해결하는 방법입니다.

컴퓨터의 자원은 한정적이어서 무한히 값을 계산할 수 없기 때문에, 이미 계산된 값의 결과를 재활용하여 문제를 해결하는 방법을 만들어 내게 되는데 이것이 dynamic programming입니다.

 

뭐가 다이나믹한 건지 의문을 제시할 수도 있는데, 이 기법을 처음 고안한 Richard Bellman은 dynamic이라는 단어가 멋있어 보여서, 벨 연구소에서 펀딩을 받기 위해 이렇게 이름을 지었기 때문에 그냥 넘어가면 됩니다. '기억하며 풀기'라고 이해하면 됩니다.

---

아래의 순서로 DP 문제를 접근해 볼 수 있습니다.

 

1. DP의 조건

DP를 이용해 문제를 해결하기 위해서는 아래 3가지 조건을 만족해야 합니다.

1. Simple Subproblems : 큰 문제를 작은 문제로 단순화할 수 있어야 합니다.
2. Overlapping Subproblems : 작은 문제들이 반복되어야 합니다.
3. Optimal Substructure : 작은 문제의 최적의 결과를 사용해 큰 문제의 최적의 결과를 도출할 수 있어야 합니다.

2. 점화식

1번의 조건을 만족한다면, 문제의 변수를 이용해 점화식을 세워 봅니다.

 

3. Top-Down / Bottom-Up 방식 중 선택

두 방식 중 하나를 선택해서 문제를 해결합니다. 뭐가 좋고 나쁘고 할 것 없이 상황에 따라 선택하면 됩니다.

• Top-Down : 큰 문제에서 작은 문제로 내려가 문제를 해결하는 방식입니다. 작은 문제로 내려갈 때 해당 문제 결과가 필요하다면, 해당 문제의 값을 계산하고 메모리에 저장해 놓습니다. 이 때 저장해 놓은 값은 나중에 결과가 또 필요해 질 때 또 사용됩니다. (새로 계산하지 않습니다.) 이렇게 값을 저장하는 방법을 Memoization(메모이제이션)이라고 합니다.
• Bottom-Up : 작은 문제에서 큰 문제로 올라가 문제를 해결하는 방식입니다. Top-Down의 memoization과의 차이는, 필요하지 않은 값도 미리 계산해 둔다는 것입니다. 이런 방식을 Tabulation(타뷸레이션)이라고 합니다.

---

Dynamic Programming을 피보나치 수열에 적용시켜 보겠습니다.

 

피보나치 수열을 Python으로 구현하면 다음과 같습니다.

def fibo(n):
    if n <= 1:
        return n
    else:
        return fibo(n - 1) + fibo(n - 2)

if __name__ == '__main__':
    n = int(input())
    fibo(n)

재귀함수를 이용해 구현한 코드입니다.

[그림 1] n = 5일 때의 피보나치 함수

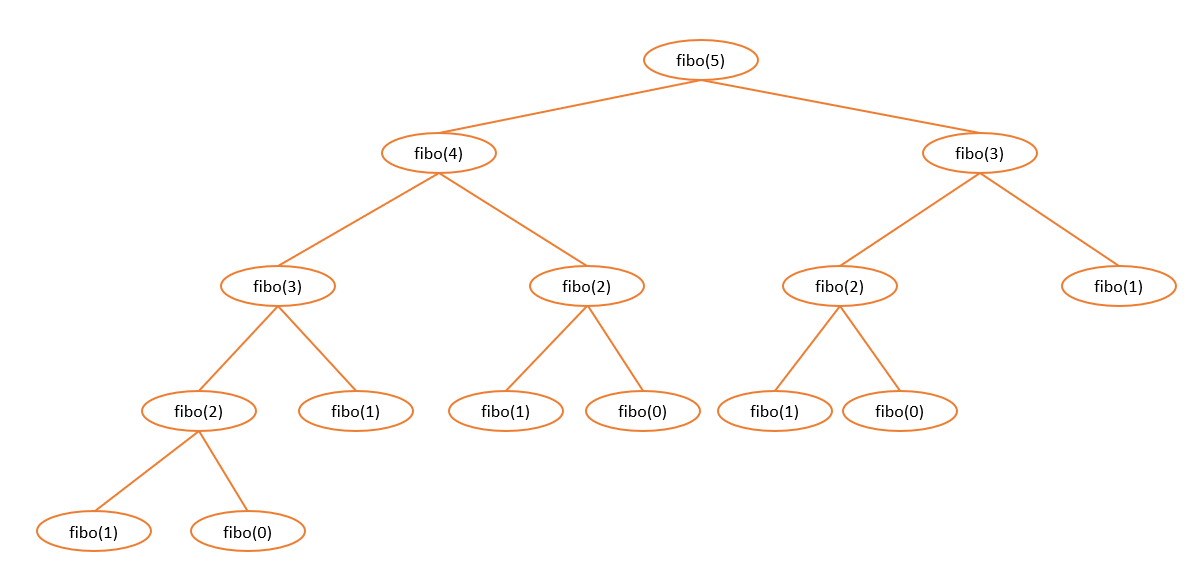
n = 5일 때 [그림 1]처럼 함수를 호출합니다.

중복해서 함수를 호출하는 부분이 있습니다. 숫자가 작으면 상관 없겠지만, 값이 커지면 계산 시간도 늘어나고 중복되는 부분도 많아지기 때문에 비효율적입니다.

 

1. 조건 확인

DP로 문제풀이가 가능한지 확인해 보겠습니다.

 

1-1. Simple Subproblems : 큰 문제를 작은 문제로 단순화할 수 있어야 합니다.

  - 해당 행렬의 수(n)를 구할 때 해당 숫자의 앞부분(n-1, n-2)들의 합으로 결과를 도출할 수 있고, 이를 fibo() 함수로 나타낼 수 있습니다.

1-2. Overlapping Subproblems : 작은 문제들이 반복되어야 합니다.

 - [그림 1]에서 fibo() 함수가 반복됨을 확인할 수 있습니다.
1-3. Optimal Substructure : 작은 문제의 최적의 결과를 사용해 큰 문제의 최적의 결과를 도출할 수 있어야 합니다.

- fibo(k)의 값이 항상 똑같은 것을 이용하여, 큰 문제를 해결할 수 있습니다.

 

2. 점화식

1번의 조건 확인으로 DP로 문제풀이가 가능함을 확인했습니다.

n번째 수열을 계산한다고 할 때, 이 n을 이용하여 점화식을 세우면 다음과 같습니다.

$$ fibo(n) = fibo(n-1) + fibo(n-2) $$

 

3. Top-Down / Bottom-Up 중 선택

두 방법 중에 하나를 선택하여 문제를 해결합니다.

이 글에서는 두 방법 각각 모두 사용하여 문제를 해결해 보겠습니다.

 

3-1. Top-Down

def fibo(n, res):
    if res[n] != 0:
        return res[n]  # fibo(n)이 이미 저장되어 있으면 해당 값 반환
    else:
        res[n] = fibo(n - 1, res) + fibo(n - 2, res)  # fibo(n)이 저장되지 않은 경우 계산하여 저장
        return res[n]

if __name__ == '__main__':
    res = [0 for i in range(100)]  # 해당 배열에 fibo() 결과 저장
    res[0] = res[1] = 1  # fibo(0), fibo(1) 값 미리 저장

    n = int(input())
    fibo(n, res)
    print(res[:n])

Top-Down 방식을 이용하여 구현한 코드입니다.

 

3-2. Bottom-Up

def fibo(n):
    res = [0 for i in range(100)]  # 해당 배열에 fibo() 결과 저장
    res[0] = res[1] = 1  # fibo(0), fibo(1) 값 미리 저장

    if n <= 1:
        return res[:n]
    
    for i in range(2, n):
        res[i] = res[i - 1] + res[i - 2]

    return res[:n]

if __name__ == '__main__':

    n = int(input())
    print(fibo(n))

Bottom-Up 방식을 이용하여 구현한 코드입니다.

 

---

해당 풀이법을 이용한 문제입니다.

https://spareone.tistory.com/63

[PS] 백준 1003번 - 피보나치 함수 | C++