1. 진법과 진수
r진법은 0부터 r-1까지의 수를 나타내는 방법입니다.
진수는 진법으로 나타낸 수를 의미하며, r진수는 r진법으로 나타낸 수가 됩니다.
2. 진법 변환
n진수에서 r진수로 변환을 할 경우 다음과 같은 방법을 사용하면 됩니다.
- 정수: r로 나누기 (나머지가 0이 될 때 까지)
- 소수: r로 곱하기 (0이 될 때 까지)
3. 2진수
컴퓨터에서는 2진수 (0과 1)를 통해 수를 표현합니다.
2진수를 사용하는 이유는 효율성 때문입니다.
회로에서는 전압 범위에 따른 전압 인가가 어렵습니다.
특정 크기의 전압을 인가하더라도 계속 그 전압이 유지된다는 보장도 없습니다.
이런 이유 때문에 '전압을 얼마나 인가하였는가'가 아닌 '전압을 인가하였는가'에 초점을 맞추어 회로를 구성하게 됩니다.
기본적으로 5V가 인가됩니다.
전기가 인가된 경우 1로 표현하며, 그렇지 않은 경우 0으로 표현합니다.
0과 1을 표현하는 기본 단위는 bit라고 표현합니다.
bit가 4개 모이면 1 nibble, bit가 8개 모이면 1 byte라고 표현합니다.

가장 왼쪽에 있는 bit를 MSB(Most Significant Bit), 가장 오른쪽에 있는 bit를 LSB(Least Significant Bit)라고 합니다.
값의 기여도가 가장 높은 bit가 왼쪽 bit이고, 기여도가 가장 낮은 bit가 오른쪽 bit이기 때문입니다.
2진수끼리의 산술 연산은 10진수에서 하던 것과 같습니다.
덧셈을 할 경우 올림수에 유의하고, 뺄셈을 할 경우 빌림수에 유의합니다.
bit를 왼쪽으로 shift(<<) 할 경우 2를 곱한 것과 동일한 값이 나옵니다.
반대로 bit를 오른쪽으로 shift(>>) 할 경우 2를 나눈 것과 동일한 값이 나옵니다.
4. 16진수
2진수는 너무 길어서 bit stream이 길게 늘어서게 됩니다.
여기서 하나의 아이디어가 나오게 됩니다.
2진수에서 4bit씩 묶으면 16진수 하나로 표현할 수 있게 됩니다. ex) 1111 -> F
이런 이유로 16진수로 변환하여 사용하는 경우가 많습니다.
16진수는 0~15의 수를 표현하게 되는데, 10부터는 대응되는 한 자리 수가 없습니다.
이를 해결하기 위해 10부터 15까지는 A~F의 알파벳을 사용하게 됩니다.
5. 8진수
2진수에서 3bit씩 묶으면 8진수 하나로 표현할 수 있습니다.
하지만 16진수 놔두고 굳이 8진수를 잘 이용하지는 않습니다.
6. 2진수의 음수 표현
2진수를 음수로 표현하기 위한 여러 아이디어가 있습니다.
6-1. 부호화 크기 표현 (부호화 절댓값 표현)
간단하게 생각해 볼 수 있는 기본적인 방법은, 최상위 bit로 부호를 표현한 부호화 크기 표현입니다.
부호화 절댓값 표현이라고도 합니다.
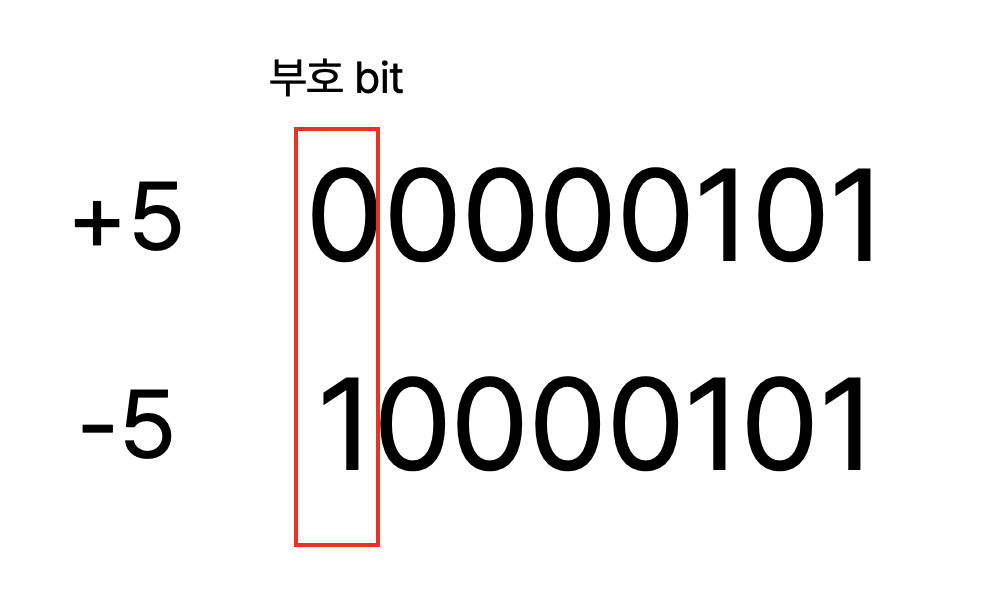
양수일 때는 0, 음수일 때는 1로 설정하여 수를 표현합니다.
가장 직관적으로 표현할 수 있는 방법입니다.
하지만 이렇게 표현하면 2가지의 0이 생깁니다. (+0, -0)
또한, 이렇게 표현된 수들을 연산할 경우
- 결과 값 부호를 정하기 위해 두 값의 절댓값을 비교해야 합니다. 이 과정에서 비교기가 필요합니다.
- 절댓값이 큰 값의 부호를 선택해야 합니다. 이 과정에서 부호 비트 선택기가 필요합니다.
- 뺄셈을 해야 할 경우 감산기가 필요합니다.
추가 회로가 필요하게 되어 회로가 복잡해지는 문제가 발생합니다.
6-2. 보수 표현
이 문제를 해결하기 위해 보수 표현 방법을 생각하게 됩니다.
보수는 어떤 수를 만드는 데 보충해 주는 수를 말합니다. 빨강이 아닙니다.
15 - 12를 한다고 하면, 15 + (-12) 로 표현을 바꿀 수 있습니다.
이것을 15 + (100 - 12) - 100으로 바꿀 수 있습니다.
여기서 (100 - 12)가 10의 보수 표현이라고 해 봅니다.
15에서 12의 10의 보수를 더한 뒤 100을 빼면 15 - 12의 결과와 같은 값이 나옵니다.
위의 원리를 이용하면 가산기만으로 뺄셈 구현이 가능합니다.
감산기 없으면 -100은 어떻게 연산하느냐? 그냥 맨 앞 자리 버리면 됩니다.

2진수에서 보수는 각 bit를 반전시켜 구할 수 있습니다.
이렇게 구한 표현을 1의 보수 표현이라고 합니다.
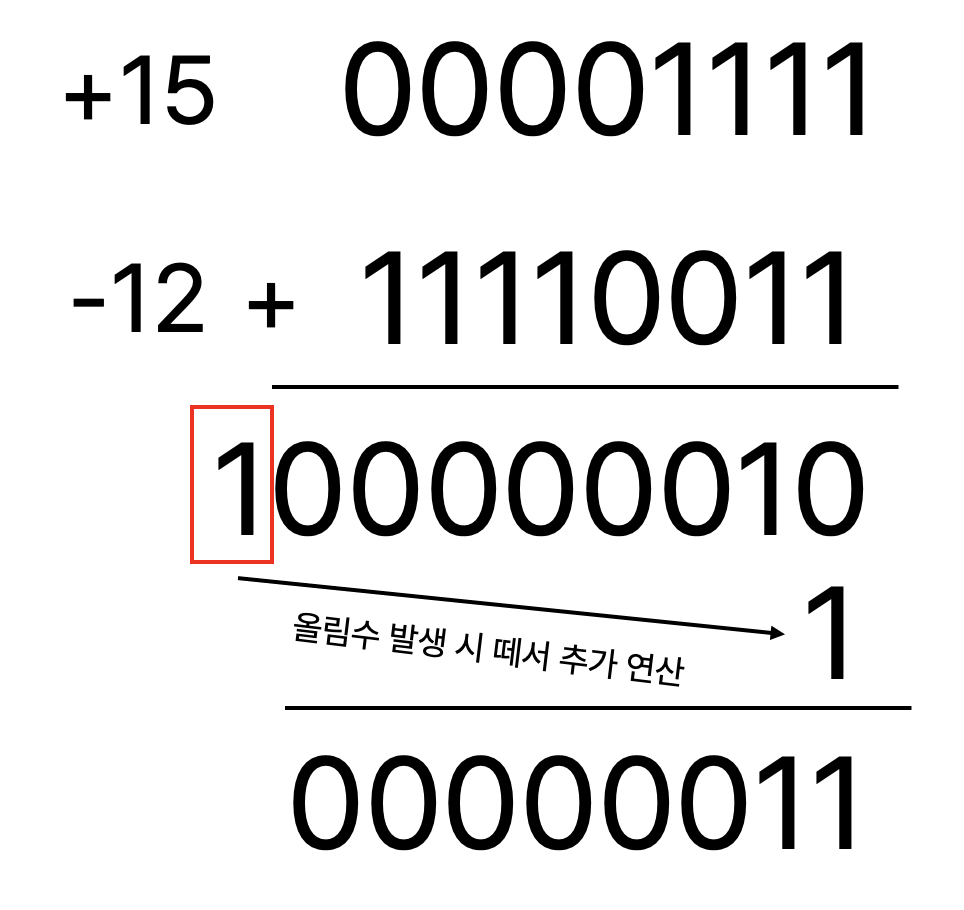
1의 보수로 연산을 할 경우 덧셈을 하면 되고, 맨 앞에 올림수가 발생하면 떼 버리고 +1을 하면 됩니다.
보수 표현을 하게 되면 위와 같이 가산기로 덧셈, 뺄셈을 모두 할 수 있다는 장점이 있습니다.
하지만 여전히 0이 2개 존재하는 (+0, -0) 문제는 해결하지 못했습니다.

이 문제를 해결하기 위해 2의 보수 표현 방식을 사용합니다.
+0과 -0이 공존하는 문제가 사라집니다.
또한, -0 대신 추가로 하나의 수를 더 표현할 수 있게 됩니다.
2의 보수는 1의 보수에서 +1을 하면 구할 수 있습니다.
더 간단한 방법으로는, 가장 오른쪽에 위치한 1의 bit 값 앞쪽 bit를 반전시키면 구할 수 있습니다.

2의 보수로 연산을 할 때에도 그대로 덧셈을 하면 됩니다.
1의 보수와는 다르게 올림수가 발생하면 다른 연산 없이 그냥 떼 버리면 됩니다.
대부분의 시스템에서는 2의 보수 표현 방식을 사용합니다.
사람이 직관적으로 볼 수는 없지만, 어짜피 연산은 컴퓨터가 합니다.
7. 오버플로우와 언더플로우
1byte (8bit)를 통해 수를 표현할 경우, 이 값의 범위는 \( (-2^{8}) \) ~ \( (2^{8} - 1) \) 입니다.
이 값의 표현 범위를 벗어나면 문제가 발생합니다.
표현 범위보다 더 커지면 overflow, 더 작으면 underflow가 발생합니다.
최상위비트의 올림수와 최상위비트 - 1의 올림수 값이 다른 경우 오버플로우 / 언더플로우가 발생합니다.
8. 소수 표현
위에서 본 것들은 모두 정수 표현을 위한 방법입니다.
컴퓨터로 실수를 표현할 경우 생각해야 하는 요소가 많습니다.
소수점을 어떻게 찍을 것인가, 부호는 어떻게 할 것인가, 몇 비트로 수를 나타낼 것인가 등 생각할 것이 많아집니다.
소수점을 어떻게 하느냐에 따라 크게 두 가지 방식을 생각해 볼 수 있습니다.
8-1. 고정 소수점
특정 구간에 소수점을 고정시키는 방식입니다.
이 방식은 시스템에서 비트의 개수, 소수점 아래 비트 개수 등의 요소를 사전에 명시가 되어 있어야 합니다.
시스템에서 사용 시 간단히 l.m 포맷 고정 소수점 표현이라고 합니다.
이 때 l = 정수부 비트 수, m = 소수부 비트 수 입니다. l과 m을 더하면 총 비트 수가 됩니다.
2진수로 바꾸고 싶은 수에 \(2^{m}\)을 곱하여 l과 m에 맞게 소수점을 찍으면 됩니다.
2진수에서 다시 돌리려면 \(2^{-m}\)을 곱하면 됩니다.
최소한의 비트로 소수를 표현할 수 있고, 비슷한 해상도를 가진 수들의 연산이 쉬워집니다.
하지만 표현의 정밀도가 떨어지기 때문에 대부분의 시스템에서는 다른 방식을 사용합니다.
8-2. 부동 소수점
수의 정확도를 높이기 위해 모든 수에 대한 표현을 정규화시키는 방식입니다.
어떤 실수든 소수점을 특정 위치로 옮겨놓은 뒤 보정 값을 곱합니다. 이렇게 하면 소수점이 달라지더라도 실수 자체는 변형되지 않습니다.
부동 소수점 표현은 IEEE에서 제정한 IEEE 754 표준 방식을 따릅니다.

32비트 표현과 64비트 표현 방식이 존재합니다.
이를 각각 IEEE 754 단정도, IEEE 754 배정도 표현 방식이라고 합니다.
C의 자료형 중 float가 단정도에 해당하고, double이 배정도에 해당합니다.
모든 실수는 1.xxxxxxxx * \( 2^{n} \) 형태로 정규화됩니다.
IEEE 754는 크게 3부분으로 나누어 표현합니다.
- 부호 (1비트)
- 부동 소수점에서의 부호 표현은 맨 왼쪽의 비트를 통해 표현합니다.
- 양수는 0, 음수는 1입니다.
- 지수부 (8비트 / 11비트)
- 가수를 정규화시킨 후의 지수 값 (소수점 옮긴 다음 보정을 위해 곱한 값의 지수)이 저장됩니다.
- 소수점에 따라 지수가 음수와 양수가 될 수 있는데, 이를 나타내기 위해 단정도에서는 127을, 배정도에서는 1023을 더하여 저장합니다.
- 127, 1023을 더하는 이유는 각 지수가 시작되는 부분의 offset이기 때문이며, 음수값을 2의 보수로 표현하지 않기 위함입니다.
- 가수부
- 소수점 아래 부분을 저장합니다.
- 단정도에서는 23비트, 배정도에서는 52비트가 할당되어 있습니다.
'논리회로' 카테고리의 다른 글
| [논리회로] 디지털 코드 (0) | 2025.04.17 |
|---|---|
| [논리회로] 신호의 종류와 논리 연산 (0) | 2025.04.16 |

댓글